发表更新Java

Java TreeMap 源码解析

在本文中，我们将详细解析 java.util.TreeMap 的源代码。本文将首先讲述红黑树及其相关操作的基本原理，并结合 TreeMap 中的相关代码加深印象，继而再对 TreeMap 中的其他代码进行详析。

为提高可读性，本文中将会在保证功能不变的情况下对 TreeMap 的源代码进行一定的修改，包括修改变量名、新增局部变量、省略重复代码等。

2-3-4 树及红黑树

首先我们看 java.util.TreeMap 的 JavaDoc 的第一句话：

A Red-Black tree based NavigableMap implementation.

由此我们了解到，TreeMap 实现了 java.util.NavigableMap 接口，其本质上的数据结构是红黑树。因此首先我们需要了解什么是红黑树。

红黑树是一种自平衡的二叉搜索树（Self-balancing Binary Search Tree）。阅读过《Algorithms》一书的读者应该了解，红黑树的思想延伸自 2-3-4 树，它们本质上是等价的，红黑树只是在使用统一的二叉树结点的基础上加上结点的颜色信息来替代 2-3-4 树中特有的 3-结点和 4-结点，而红黑树的相关操作实际上也都一一对应着 2-3-4 树的操作。因此，本文将结合讲解 2-3-4 树的相关操作以加深读者对红黑树的理解。除此之外，2-3-4 树实际上就是一种特殊的 B 树，理解 2-3-4 树对读者后续理解 B 树也大有裨益。

通过阅读 2-3-4 树的维基百科可知，2-3-4 树是一种完美平衡的搜索树，除普通的二叉结点，或 2-结点外，还包含了分别有 3 个和 4 个子结点的 3-结点和 4-结点：

2-结点 3-结点 4-结点

而红黑树则是通过为结点间的链接赋予颜色属性来使用二叉结点表示 2-3-4 树。但在计算机语言实现中，难以表示链接（指针）的颜色，因此就将颜色信息储存在了结点中，以表示由父结点指向该结点的链接的颜色。当一个黑色父结点只有一个红色子结点时，这两个结点代表了 2-3-4 树中的一个 3-结点，两个结点的一共 3 个子结点对应 3-结点的 3 个子结点；当一个黑色父结点有两个红色子结点时，这三个节点代表了一个 4-结点，两个子结点的一共 4 个子结点则代表了 4-结点的 4 个子结点。

我们通过阅读红黑树的维基百科可以了解到，红黑树满足如下性质：

  1. 每个结点的颜色为红色或黑色
  2. 根节点的颜色为黑色
  3. 若某个结点的颜色为红色，那么它的两个孩子结点的颜色必为黑色，即不存在两对连续的红色结点
  4. 对于任意给定的内部结点，所有从该结点到位于其子树内的叶子结点的路径所经过的黑色结点数相同

其中，性质 1 定义了树结点的颜色属性；性质 2 本身意义并不大 —— 实际上根节点的颜色对红黑树的性质影响极小，该性质完全可以被忽略；而性质 3 和 4 则是确保一颗红黑树为平衡二叉搜索树的有力约束，同时红黑树的性质 4 实际上等价于等价 2-3-4 树的完美平衡性。除此之外，我们可以由性质 4 推得，根节点到最远叶结点的距离不大于由根节点到最近叶结点的距离的两倍，因此一棵红黑树只是在大致上是平衡的。

平衡树操作 —— 查找

对于 2-3-4 树而言，其本质上也是一棵搜索树，在遇到 3-结点和 4-结点时只需要通过键的大小选择合适的子结点继续向下查找即可，思想上与一般的二叉搜索树无异。

对于红黑树来说，不考虑其自平衡的特性，其本身也是一棵二叉搜索树，因此红黑树的查找操作与一般二叉搜索树无异。形式化来说，红黑树的查找操作可如下表述：

如果树是空的，则查找未命中（返回 null）；如果被查找的键与根结点的键相等，查找命中（返回对应值）；否则就（递归地）在合适的子树中继续查找：如果被查找的键较小就选择左子树，较大则选择右子树。

TreeMap 的 get(K key) 方法实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public V get(Object key) {
    Entry<K, V> p = getEntry(key);
    return (p == null ? null : p.value);
}

final Entry<K, V> getEntry(Object key) {
    // Offload comparator-based version for sake of performance
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
    Entry<K, V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

final Entry<K, V> getEntryUsingComparator(Object key) {
    @SuppressWarnings("unchecked")
        K k = (K) key;
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        Entry<K, V> p = root;
        while (p != null) {
            int cmp = cpr.compare(k, p.key);
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
                p = p.right;
            else
                return p;
        }
    }
    return null;
}

除去针对自定义 Comparator 或 Comparable 键的独立实现外，TreeMap#get 方法的实现并无太特别的地方。

平衡树操作 —— 插入

自平衡二叉树的自平衡机制在结点数量发生变化时便会被触发，具体来说就是插入结点和删除结点的时候。

2-3-4 树的插入操作可形式化地描述如下：

首先从 2-3-4 树的根节点递归地向下寻找插入的位置：

  1. 如果当前结点为一个 4-结点：
    • 暂存位于 4-结点中间的键值，并将其移除，以将该结点变为一个 3-结点
    • 将该 3-结点分裂为两个 2-结点
    • 如果该结点为根节点，那么就用暂存的中间键值创建一个新的 2-结点链接分裂得出的两个 2-结点，并将该新结点作为新的根节点。树的高度增加 1，回到根节点继续递归
    • 否则就将暂存的中间键值插入到父结点（2-结点变 3-结点，3-结点变 4-结点），并由该父结点链接分裂得出的两个 2-结点。树的高度增加 1，回到父节点继续递归
  2. 继续查找其区间包含待插入键值的子结点
  3. 如果该子结点为叶子结点，便直接将键值插入到该结点中，结束递归
    • 否则，进入对应的子结点并重复递归

大致的过程可以参考这里。

对于红黑树而言，在插入前，我们采用与一般二叉搜索树相同的机制寻找新叶结点插入的位置，并在插入后将其颜色置为红色，即对应 2-3-4 树中将子结点升阶的一般操作（2-结点变 3-结点，3-结点变 4-结点）。值得注意的是，该动作不会使红黑树的性质 4 失效（新插入的红色结点不影响任意路径经过的黑色结点数），但有可能使性质 3 失效（父结点同为红色结点时，出现连续的两个红色结点）。此时为使性质 3 重新成立，具体采用什么动作则需要分情况讨论。

深刻了解红黑树操作的读者可以直接看后面的总结部分。

在详细分析每种情形前，我们先来看看 TreeMap#put 方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public V put(K key, V value) {
    Entry<K, V> t = root;
    if (t == null) { // 树为空，将新结点作为根结点
        compare(key, key); // type (and possibly null) check

        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K, V> parent;
    Comparator<? super K> cpr = comparator;
    if (cpr != null) { // 使用 Comparator 定位插入位置
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value); // 在内部结点中找到了相同的键，直接替换结点的值
        } while (t != null);
    }
    else { // 使用 Comparable#compareTo 方法定位插入位置。效果与上述代码等价
        // ...
    }
    Entry<K, V> e = new Entry<>(key, value, parent);
    // 将新结点插入叶结点的对应链接
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    // 修复红黑树
    fixAfterInsertion(e);

    size++;
    modCount++;
    return null;
}

private void fixAfterInsertion(Entry<K, V> n) {
    n.color = RED; // 新结点置为红色

    while (n != null && n != root && n.parent.color == RED) { // 向上递归修复直至遇到黑色结点
        if (parentOf(n) == leftOf(parentOf(parentOf(n)))) {
            // ...
        } else {
            // ...
        }
    }
    root.color = BLACK; // 根结点置为黑色
}

为方便表述，下文将用叔父结点（Uncle Node）来表示某个结点的父结点的兄弟结点（Sibling Node）。

红黑树插入情形 1：插入空树

当插入前红黑树为空时，需将新的结点作为红黑树的根结点。该情形已由 TreeMap#put 方法本身所处理。

红黑树插入情形 2：父结点为黑色

如果插入了新结点后，新结点的父结点为黑色，对应于 2-3-4 树中将新键值插入到了 2-结点使其成为 3-结点的情形。这实际上不会破坏 2-3-4 树的平衡性，新的结点不是 4-结点也不需要进行分裂，也没有违反红黑树的性质 3。此外，性质 4 也没有违反，因为新插入的结点为红色结点，不会影响根结点到任意叶子结点所经过的黑色结点的数量。

TreeMap#fixAfterInsertion 方法的内部 while 循环会先判断当前扫描结点的父结点颜色是否为红色。当父结点颜色为黑色时，控制流不会进入 while 循环体。

红黑树插入情形 3：父结点与叔父结点均为红色结点

由于父结点与新插入的叶子结点同为红色，性质 3 不再成立，此时便需要启动修复。实际上，由于修复过程是自底向上递归进行的，是否进入该情形与当前结点 $N$ 的颜色无关，但 $N$ 实际上却是只会是红色的。这种情形对应于 2-3-4 树中遇到 4-结点的情形（由 $P$、$U$、$G$ 共同组成的 4-结点），因此此时我们需要对 4-结点进行分裂，并把中间键值（$G$）插入到上一级结点中。

实际上，我们只需要将父结点和叔父结点的颜色反转（置为黑色），并将它们的父结点（新叶子结点的爷爷结点）置为红色即可使性质 3 和性质 4 在该子树内重新成立。如下图所示：

若如图中所示，修复后，爷爷结点 $G$ 变为红色，代表插入到了上一层的结点中，而 $P$ 和 $U$ 变为黑色，代表成为了分裂后的 2-结点，而红色的 $N$ 结点也代表了新键值插入 2-结点产生 3-结点的过程。若爷爷结点 $G$ 为红黑树的根结点，那么即修复成功。若 $G$ 不是根结点，那么我们只能确保性质 3 和 4 在以 $G$ 为根的子树内成立，在 $G$ 往上的树中并不一定成立，因此我们需要继续从 $G$ 开始递归地向上修复。

TreeMap#fixAfterInsertion 方法中的相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
while (n != null && n != root && n.parent.color == RED) {
    if (parentOf(n) == leftOf(parentOf(parentOf(n)))) {
        // g = parentOf(parentOf(n))
        Entry<K, V> u = rightOf(parentOf(parentOf(n)));
        if (colorOf(u) == RED) {
                setColor(parentOf(n), BLACK); // p = parentOf(n)
                setColor(u, BLACK);
                setColor(parentOf(parentOf(n)), RED);
                n = parentOf(parentOf(n));
        } else {
            // ...
        }
    } else {
        // 与上半部分代码相对称 
    }
}

子树的左旋转与右旋转

对接下来的两种不平衡情形的修复涉及到了对子树的旋转操作。旋转操作会保持二叉搜索树性质的情况下反转指定父子结点的父子关系，即原本的子结点升级为父结点，父结点降级为子结点，而两个结点原本的其他子结点及子树则基于一定的规则重新分配。

以左旋转为例，父结点 P 与其右子结点 Q 一同逆时针旋转，原本的父结点 P 将变为右子结点 Q 的左子结点。除此之外，Q 原本的左子结点 B 将成为 P 的左子结点。如下图所示：

右旋转则为左旋转的逆过程。

在 TreeMap 中，左旋转与右旋转分别对应于方法 rotateLeft 和 rotateRight，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
private void rotateLeft(Entry<K, V> p) {
    if (p != null) {
        Entry<K, V> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

private void rotateRight(Entry<K, V> p) {
    if (p != null) {
        Entry<K, V> l = p.left;
        p.left = l.right;
        if (l.right != null) l.right.parent = p;
        l.parent = p.parent;
        if (p.parent == null)
            root = l;
        else if (p.parent.right == p)
            p.parent.right = l;
        else p.parent.left = l;
        l.right = p;
        p.parent = l;
    }
}

红黑树插入情形 4：叔父结点为黑色结点，当前结点与其父结点及爷爷结点间形成左左结构

在该情形下，父结点为红色结点，但叔父结点为黑色结点。除此之外，当前结点为父结点的左子结点，而父结点同为爷爷结点的左子结点，即这三代结点形成了左左结构。

此时，我们需要将父结点与爷爷结点的颜色互换，并以爷爷结点为锚点执行右旋转操作。如下图所示：

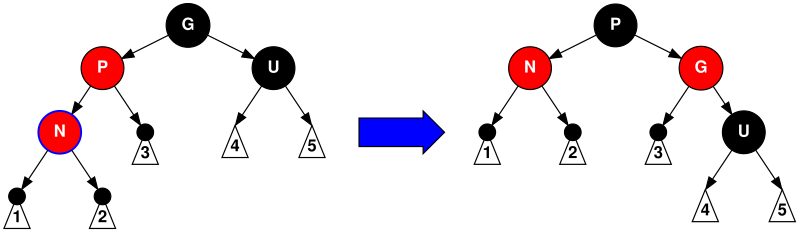
对于 2-3-4 树而言，原本的两个连续的红色结点无法代表 2-3-4 树的结点，但在经过旋转和变色后，$N$、$P$、$G$ 则重新构成了一个 4-结点，因此我们仍需以上升后的 $N$ 结点为起点向上递归修复，触发下一次的 4-结点分裂。

若三代结点间形成的是右右结构，我们只需要轴对称地执行左旋转操作即可。

TreeMap#fixAfterInsertion 方法中的相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
while (n != null && n != root && n.parent.color == RED) {
    if (parentOf(n) == leftOf(parentOf(parentOf(n)))) {
        Entry<K, V> u = rightOf(parentOf(parentOf(n)));
        if (colorOf(u) == RED) {
            // ...
        } else {
            if (n == rightOf(parentOf(n))) {
                // ...
            }
            setColor(parentOf(n), BLACK);
            setColor(parentOf(parentOf(n)), RED);
            rotateRight(parentOf(parentOf(n)));
        }
    } else {
        // 与上半部分轴对称
    }
}

红黑树插入情形 5：叔父结点为黑色结点，当前结点与其父结点及爷爷结点间形成左右结构

在该情形下，父结点为红色结点，但叔父结点为黑色结点。除此之外，当前结点为父结点的右子结点，而父结点则为爷爷结点的左子结点，即这三代结点形成了左右结构。

此时，我们需要以父结点为锚点执行左旋转操作。如下图所示：

实际上这项操作并未使得子树得以修复，而是使得当前的结构进入了情形 4，因此我们需要再次执行情形 4 对应的修复动作。同理，原本的两个连续的红色结点无法代表 2-3-4 树的结点，因此我们需要进入情形 4 再执行对应修复，以重新得到一个合法的红黑树。

若三代结点间形成的是右左结构，我们只需要轴对称地执行右旋转即可。

TreeMap#fixAfterInsertion 方法中的相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
while (n != null && n != root && n.parent.color == RED) {
    if (parentOf(n) == leftOf(parentOf(parentOf(n)))) {
        Entry<K, V> u = rightOf(parentOf(parentOf(n)));
        if (colorOf(u) == RED) {
            // ...
        } else {
            if (n == rightOf(parentOf(n))) { // 进入情形 5
                n = parentOf(n);
                rotateLeft(n);
            }
            // 进入情形 4，继续修复
            setColor(parentOf(n), BLACK);
            setColor(parentOf(parentOf(n)), RED);
            rotateRight(parentOf(parentOf(n)));
        }
    } else {
        // 与上半部分轴对称
    }
}

总结

红黑树插入修复的总结如下：

# 情形 处理 示意图
2 $P$ 为黑色结点 结束修复
3 $P$ 和 $U$ 均为红色结点 将 $P$、$U$、$G$ 的颜色反转。 $G$ 的颜色变为红色，故从 $G$ 开始继续往上执行相同的修复过程
4 $U$ 为黑色结点，$G$、$P$、$N$ 形成左左结构 $P$、$G$ 颜色互换，并以 $G$ 进行右旋转
5 $U$ 为黑色结点，$G$、$P$、$N$ 形成左右结构 以 $P$ 进行左旋转，从 $P$ 开始继续修复，进入情形 4

TreeMap#fixAfterInsertion 方法的总结如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
private void fixAfterInsertion(Entry<K, V> n) {
    n.color = RED; // 新结点置为红色

    while (n != null && n != root && n.parent.color == RED) {
        Entry<K, V> p = parentOf(n);
        Entry<K, V> g = parentOf(p);
        if (p == leftOf(g)) {
            Entry<K, V> u = rightOf(g);
            if (colorOf(u) == RED) {   // 进入情形 3，进行颜色反转
                setColor(p, BLACK);
                setColor(u, BLACK);
                setColor(g, RED);
                // 递进至爷爷结点，即新出现的红色结点，继续向上修复
                n = g;
            } else {
                if (n == rightOf(p)) { // 进入情形 5，以父结点进行左旋转
                    n = p;
                    rotateLeft(n);
                }
                setColor(p, BLACK);    // 进入情形 4。设置颜色后，以爷爷结点进行右旋转
                setColor(g, RED);
                rotateRight(g);
            }
        } else {
            // 与上半部分代码轴对称
            Entry<K, V> u = leftOf(g);
            if (colorOf(u) == RED) {  // 进入情形 3
                setColor(p, BLACK);
                setColor(u, BLACK);
                setColor(g, RED);
                n = g;
            } else {
                if (n == leftOf(p)) { // 进入情形 5，以父结点进行右旋转
                    n = p;
                    rotateRight(n);
                }
                setColor(p, BLACK);   // 进入情形 4。设置颜色后，以爷爷结点进行左旋转
                setColor(g, RED);
                rotateLeft(g);
            }
        }
    }
    root.color = BLACK // 将根结点置为黑色
}

平衡树操作 —— 删除

与插入操作同理，在删除前，我们采用与一般二叉搜索树相同的方法查找需要删除的元素。与之不同的是，我们不会直接执行原地删除操作，因为待删除的结点有可能是内部结点，而新插入的结点只可能是叶子结点，因此要完成删除操作还需要一些特殊的预处理。

当删除内部结点时，我们采取与一般二叉搜索树相同的方法，先将其与其后继结点（Successor Node）互换（颜色保持不变），再删除该后继结点。后继结点通常指大于该结点的最小结点或小于该结点的最大结点。对于一个同时有着左右子结点的结点来说，其后继结点即为位于其右子树最左下角的结点或位于其左子树最右下角的结点。因此在完成该预处理后，我们只需要考虑待删除结点只有一个子结点或没有子结点（叶子结点）两种情况。

对于一般的二叉搜索树而言，删除有一个子结点的内部结点只需要让其父结点的对应链接直接指向该子结点即可。而删除叶子结点的操作则更是简单了。

首先我们考虑 2-3-4 树的删除操作。形式化的描述如下：

  1. 查找待删除的键值
    • 如果键值所处结点不是叶子结点，那就继续向下递归寻找其后续结点，同时在下沉的过程中对结点进行调整，以确保所找到的后续结点不是一个 2-结点
    • 如果键值所处的结点是一个 2-叶子结点，那就对结点进行相同的调整

在下降的过程中对沿途所有非根结点的 2-结点 $N$ 作如下调整：

  1. 如果父结点 $P$ 和兄弟结点 $S$ 均为 2-结点，那就将 $N$、$P$、$S$ 组合成一个 4-结点，树的高度减少 1。实际上，这种情况只有在父结点 $P$ 同为根结点时才会发生，
    因为其他 2-结点在下降的过程中早已被转换
  2. 如果有一个位于该结点左侧或右侧的兄弟 3-结点或 4-结点 $S$（即包含多于一个的键值），那么就与该兄弟结点进行旋转操作：
    • 将兄弟结点 $S$ 距离该结点 $N$ 最近的键值上升到两个结点的父结点 $P$ 中
    • 父结点 $P$ 原有的键值下降到该 2-结点 $N$ 中以形成一个 3-结点
    • 原本属于上升至父结点的键值的子结点现在成为 $N$ 的新的子结点
  3. 如果父结点 $P$ 为 3-结点或 4-结点且所有兄弟结点均为 2-结点，那么就将 $N$、$P$ 以及其最近的兄弟结点 $S$ 执行混合操作：
    • 利用 $N$ 的键值、 $S$ 的键值以及 $P$ 中位于 $N$ 和 $S$ 链接交合处的键值（一共三个键值）组成一个 4-结点
    • 将 $S$ 原本的子结点变为该结点的子结点

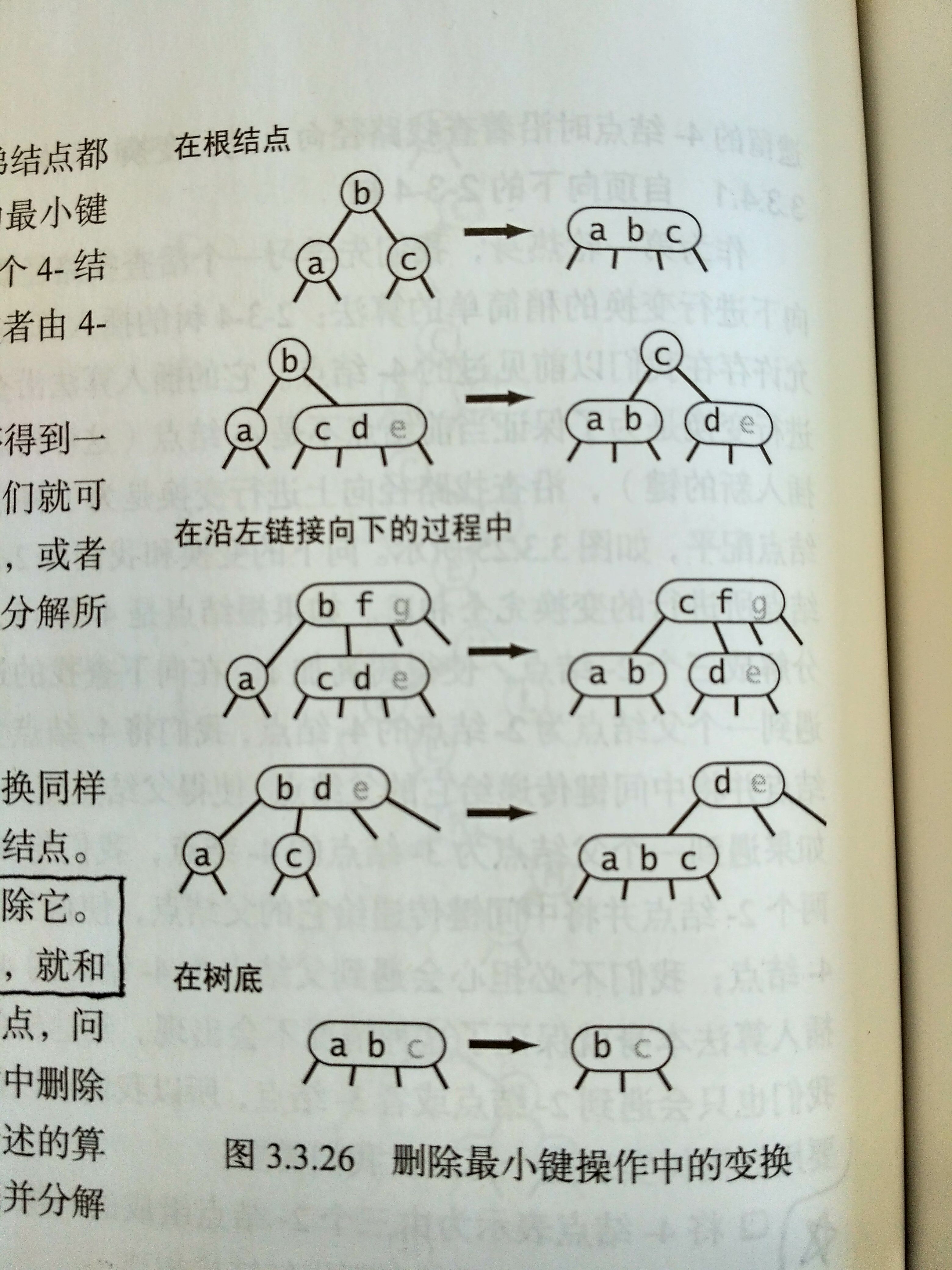
如此一来，待删除键值所处的叶子结点便不是 2-结点（包含多于一个键值），可以安全地将其移除并对该叶子结点进行降阶，同时不影响 2-3-4 树的平衡性。该过程结合《Algorithms》一书的图 3.3.26 应该会更好理解。（见右侧）

但对于红黑树而言，如果被移除的结点是一个黑色结点则有可能使得性质 3 和 4 不再成立，因此需要在此时对红黑树进行修复。

我们先对可能发生的情况进行讨论：

  • 待删除的结点为红色结点：这种情况对应于 2-3-4 树中的一般结点降阶过程。那么由性质 3 可知，它的父结点和子结点必为黑色结点，而从红黑树内部移除一个红色结点不会改变根结点到任意叶子结点所经过黑色结点的数量，因此性质 4 也不会变化，在这种情况下我们不需要进行任何修复；
  • 待删除结点为黑色结点，其子结点为红色结点：这种情况同样对应于 2-3-4 树中的一般结点降阶过程。但由它的红色子结点会顶替它原有的位置，这会导致红黑树的性质 4 不成立（通过该结点的所有路径所经过的黑色结点数减少 1），此时我们只需要将该子结点置为黑色即可使性质 4 重新成立。

TreeMap#remove 方法的相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public V remove(Object key) {
    Entry<K, V> p = getEntry(key); // 查找待删除的结点
    if (p == null)                 // 结点不存在，返回
        return null;

    V oldValue = p.value;
    deleteEntry(p);                // 删除结点
    return oldValue;
}

private void deleteEntry(Entry<K, V> p) {
    modCount++;
    size--;

    if (p.left != null && p.right != null) { // 待删除结点是有两个子结点的内部结点
        Entry<K, V> s = successor(p);   // 与后继结点替换
        p.key = s.key;
        p.value = s.value;
        p = s;                          // 开始删除该后继结点
    }

    // 到这里，p 所指向的结点只可能有 1 个或 0 个子结点

    Entry<K, V> replacement = (p.left != null ? p.left : p.right); // 获取其子结点作为替换结点

    if (replacement != null) { // 替换结点不为空，即 p 有一个子结点
        replacement.parent = p.parent; // 用替换结点替换 p
        if (p.parent == null)   // p 为根结点
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;
        p.left = p.right = p.parent = null;

        if (p.color == BLACK) // 若被删除的结点为黑色结点，执行自平衡修复
            fixAfterDeletion(replacement);
    } else if (p.parent == null) { // p 为叶子结点，且 p 为根结点，即此时红黑树只有一个结点
        root = null;
    } else { // p 为叶子结点
        if (p.color == BLACK) // 若被删除的结点为黑色结点，执行自平衡修复
            fixAfterDeletion(p);

        if (p.parent != null) { // 移除 p
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

我们可以看一下 TreeMap#fixAfterDeletion 方法的循环结束条件：

1
2
3
4
5
6
private void fixAfterDeletion(Entry<K, V> n) {
    while (n != root && colorOf(n) == BLACK) { // 当 n 为根结点或红色结点时结束循环
        // ...
    }
    setColor(n, BLACK); // 对于上面提到的第二种情形，红色子结点会在这里被置为黑色
}

接下来我们就需要分情况讨论待删除结点及其子结点同为黑色结点的情况了，即在 2-3-4 树中删除 2-结点的情况。出于方便，接下来我们将作为修复起点的结点称为 $N$，其父结点为 $P$，兄弟结点为 $S$，并有 $S$ 结点的左右子结点分别为 $S_L$ 和 $S_R$。

红黑树删除情形 1：兄弟结点 S 为红色结点

在这种情况下，我们需要以父结点 $P$ 为锚点进行左旋转，让兄弟结点 $S$ 变为当前结点 $N$ 的爷爷结点，再将 $P$ 置为红色，$S$ 置为黑色即可。如下图所示：

TreeMap#fixAfterDeletion 方法的相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private void fixAfterDeletion(Entry<K, V> n) {
    Entry<K, V> p = parentOf(n);
    while (n != root && colorOf(n) == BLACK) {
        if (n == leftOf(p)) {
            Entry<K, V> s = rightOf(p);
            Entry<K, V> s_l = leftOf(s);
            Entry<K, V> s_r = rightOf(s);

            if (colorOf(s) == RED) { // 进入情形 1
                setColor(s, BLACK);
                setColor(p, RED);
                rotateLeft(p);
                s = rightOf(p);
                s_l = leftOf(s);
                s_r = rightOf(s);
            }

            // ...

        } else { // 与上半部分代码轴对称
            // ...
        }
    }

    setColor(n, BLACK);
}

此时我们并未完成修复，因为由于黑色结点被删除，经过 $N$ 的路径仍然比经过 $S_L$ 的路径少一个黑色结点，因此我们仍然需要以 $N$ 为起点进行修复，但此时则进入了其他情形（取决于原 $S_L$ 的颜色）。

红黑树删除情形 2：兄弟结点及其子结点均为黑色结点

此时，由于被删除结点的关系，经过结点 $N$ 的路径少了一个黑色结点。此时我们需要将兄弟结点 $S$ 置为红色，如下图所示：

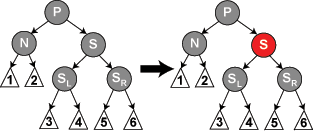
这对应于在 2-3-4 树中将两个 2-结点合并为一个 3-结点的过程。即便如此，我们也只是确保了性质 4 在以 $P$ 为根的子树内成立，我们仍需要继续以 $P$ 为起点向上修复。

TreeMap#fixAfterDeletion 方法中的相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

private void fixAfterDeletion(Entry<K, V> n) {
    Entry<K, V> p = parentOf(n);
    while (n != root && colorOf(n) == BLACK) {
        if (n == leftOf(p)) {
            Entry<K, V> s = rightOf(p);
            Entry<K, V> s_l = leftOf(s);
            Entry<K, V> s_r = rightOf(s);

            if (colorOf(s) == RED) {
                // ...
            }

            if (colorOf(s_l)  == BLACK &&
                colorOf(s_r) == BLACK) { // 进入情形 2
                setColor(s, RED);        // 兄弟结点置为红色
                n = p;                   // 继续从父结点开始向上修复
            } else {
                // ...
            }
        } else { // 与上半部分代码轴对称
            // ...
        }
    }

    setColor(n, BLACK);
}

红黑树删除情形 3：兄弟结点及其右子结点为黑色结点，其左子结点为红色结点

此时，我们以 $S$ 为锚点执行右旋转，并将 $S_L$ 与 $S$ 的颜色互换，继而进入情形 4。如下图所示：

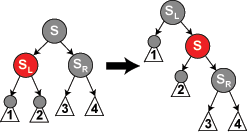
TreeMap#fixAfterDeletion 方法中的相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
private void fixAfterDeletion(Entry<K, V> n) {
    Entry<K, V> p = parentOf(n);
    while (n != root && colorOf(n) == BLACK) {
        if (n == leftOf(p)) {
            Entry<K, V> s = rightOf(p);
            Entry<K, V> s_l = leftOf(s);
            Entry<K, V> s_r = rightOf(s);

            if (colorOf(s) == RED) {
                // ...
            }

            if (colorOf(s_l)  == BLACK &&
                colorOf(s_r) == BLACK) {
                // ...
            } else {
                if (colorOf(s_r) == BLACK) { // 进入情形 3
                    setColor(s_l, BLACK);
                    setColor(s, RED);
                    rotateRight(s);
                    s = rightOf(p);
                    s_l = leftOf(s);
                    s_r = rightOf(s);
                }
                // ...
            }
        } else { // 与上半部分代码轴对称
            // ...
        }
    }

    setColor(n, BLACK);
}

红黑树删除情形 4：兄弟结点及其左子结点为黑色结点，其右子结点为红色结点

在这种情况下，我们在结点 $P$ 上做左旋转，并互换 $P$ 和 $S$ 的颜色，再将 $S_R$ 置为黑色。

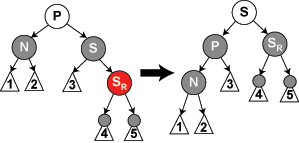
如此一来，由于 $N$ 新增了一个新的黑色父结点 $P$，原本经过 $N$ 的路径的黑色结点数得到了恢复，同时由于 $S_R$ 的颜色变为了黑色，经过 $S_R$ 的路径的黑色结点数也没有变化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
private void fixAfterDeletion(Entry<K, V> n) {
    Entry<K, V> p = parentOf(n);
    while (n != root && colorOf(n) == BLACK) {
        if (n == leftOf(p)) {
            Entry<K, V> s = rightOf(p);
            Entry<K, V> s_l = leftOf(s);
            Entry<K, V> s_r = rightOf(s);

            if (colorOf(s) == RED) {
                // ...
            }

            if (colorOf(s_l)  == BLACK &&
                colorOf(s_r) == BLACK) {
                // ...
            } else {
                if (colorOf(s_r) == BLACK) {
                    // ...
                }
                setColor(s, colorOf(p));
                setColor(p, BLACK);
                setColor(s_r, BLACK);
                rotateLeft(p);
                n = root; // 结束循环
            }
        } else { // 与上半部分代码轴对称
            // ...
        }
    }

    setColor(n, BLACK);
}

总结

我们定义待删除的结点为 $D$、其唯一子结点为 $N$、父结点为 $P$、爷爷结点为 $G$、兄弟结点为 $S$，那么红黑树删除修复可总结如下：

# 情形 处理 示意图
$D$ 为红色结点 无需修复
$D$ 为黑色结点，$N$ 为红色结点 $N$ 置为黑色，结束修复
1 $D$、$N$ 为黑色结点，$S$ 为红色结点 以 $P$ 进行左旋转，$P$、$S$ 进行颜色互换，使 $N$ 的父结点为红色结点

TreeMap#fixAfterDeletion 方法的总结如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
private void fixAfterDeletion(Entry<K, V> n) {
    Entry<K, V> p = parentOf(n);
    while (n != root && colorOf(n) == BLACK) {
        if (n == leftOf(p)) {
            Entry<K, V> s = rightOf(p);
            Entry<K, V> s_l = leftOf(s);
            Entry<K, V> s_r = rightOf(s);

            if (colorOf(s) == RED) { // 进入情形 1，以 P 进行左旋转
                setColor(s, BLACK);
                setColor(p, RED);
                rotateLeft(p);
                s = rightOf(p);
                s_l = leftOf(s);
                s_r = rightOf(s);
            }

            if (colorOf(s_l)  == BLACK &&
                colorOf(s_r) == BLACK) { // 进入情形 2，将 S 置为红色，向上递归
                setColor(s, RED);
                n = p;
            } else {
                if (colorOf(s_r) == BLACK) { // 进入情形 3，以 S 进行右旋转
                    setColor(s_l, BLACK);
                    setColor(s, RED);
                    rotateRight(s);
                    s = rightOf(p);
                }
                setColor(s, colorOf(p));  // 进入情形 4，以 P 进行左旋转，结束修复
                setColor(p, BLACK);
                setColor(s_r, BLACK);
                rotateLeft(p);
                n = root;
            }
        } else { // 与上半部分代码轴对称
            Entry<K, V> s = leftOf(p);
            Entry<K, V> s_l = leftOf(s);
            Entry<K, V> s_r = rightOf(s);

            if (colorOf(s) == RED) { // 进入情形 1，以 P 进行右旋转
                setColor(s, BLACK);
                setColor(p, RED);
                rotateRight(p);
                s = leftOf(p);
                s_l = leftOf(s);
                s_r = rightOf(s);
            }

            if (colorOf(s_r) == BLACK &&
                colorOf(s_l) == BLACK) { // 进入情形 2，将 S 置为红色，向上递归
                setColor(s, RED);
                n = p;
            } else {
                if (colorOf(s_l) == BLACK) { // 进入情形 3，以 S 进行左旋转
                    setColor(s_r, BLACK);
                    setColor(s, RED);
                    rotateLeft(s);
                    s = leftOf(p);
                }
                setColor(s, colorOf(p)); // 进入情形 4，以 P 进行右旋转，结束修复
                setColor(p, BLACK);
                setColor(s_l, BLACK);
                rotateRight(p);
                n = root;
            }
        }
    }

    setColor(n, BLACK);
}

没理解为什么这些东西要这么做？没关系，我也不理解，可能写这些代码的人自己也不理解 =。= 实际上这些 private 方法大多数都有 /** From CLR */ 的注释，在 TreeMap.java 中也能找到这么一段注释：

1
2
3
4
5
6
7
8
9
/**
 * Balancing operations.
 *
 * Implementations of rebalancings during insertion and deletion are
 * slightly different than the CLR version.  Rather than using dummy
 * nilnodes, we use a set of accessors that deal properly with null.  They
 * are used to avoid messiness surrounding nullness checks in the main
 * algorithms.
 */

因此，此 CLR 指的应该就是 Common Language Runtime，这些自平衡代码也很有可能是从 C# 那边“借”来的。详见这里。不管怎么说，红黑树都是很复杂的数据结构，如果你不能完全记忆这些操作那就罢了，没什么必要。

Java TreeMap 源码解析

https://mr-dai.github.io/java_collection_treemap/

作者

Robert Peng

发布于

2017-02-27

更新于

2017-02-27

许可协议

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

标签

Bash1
Bigtable1
GC1
Git1
Go3
Gradle1
Groovy5
HBase1
Hadoop1
Hive ThriftServer2
JVM1
Java6
Linux1
MIT 6.8247
Mesos1
MongoDB6
Paxos2
Python2
Raft2
SQL1
Spark13
Spark SQL1
SparkSQL10
Windows1
Yarn1
ZooKeeper1
etcd1
主从备份1
分布式共识2
分布式内存1
分布式存储7
分布式系统12
分布式计算2
团队协作1
集群资源调度2
×